Matlab学习02
发表于：2022-08-12 | 分类： 程序设计 Matlab

管理会话的命令

MATLAB提供了各种用于管理会话的命令。下表提供了所有这些命令 -

命令 描述说明
clc 清除命令窗口
clear 从内存中删除变量
exist 检查文件或变量是否存在
global 声明变量为全局变量
help 搜索帮助主题
lookfor 搜索帮助关键字的条目。
quit 停止MATLAB
who 列出当前变量
whos 列出当前变量(长显示详细信息)

使用系统命令

MATLAB提供了各种有用的命令来处理系统，比如将工作区中的当前工作保存为文件，稍后加载文件。

它还为其他系统相关活动提供各种命令，如显示日期，列出目录中的文件，显示当前目录等。

下表显示了一些常用的系统相关命令 -

命令 描述说明
cd 更改当前目录(进入指定目录)
date 显示当前日期
delete 删除文件
diary 打开/关闭日记文件记录
dir 列出当前目录下的所有文件
load 从文件加载工作区变量
path 显示搜索路径
pwd 显示当前目录
save 将工作空间变量保存在文件中
type 显示文件的内容
what 列出当前目录中的所有MATLAB文件
wklread 读取.wk1电子表格文件

控制数字显示格式命令，只改变显示格式，数值不会改变

format + 数据类型

format shot(默认)

format long

format rat(小数分数显示)

1
2
3
4
5
6
7
>> 1/3
ans =
    0.3333
>> format rat
>> 1/3
ans =
       1/3

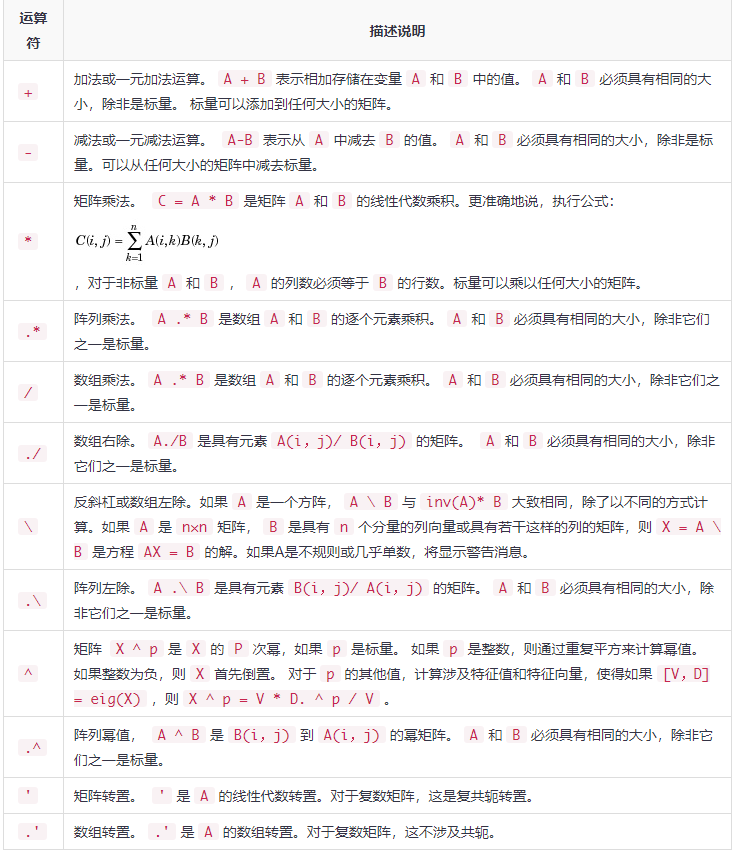
算数运算符

image-20220811234109104

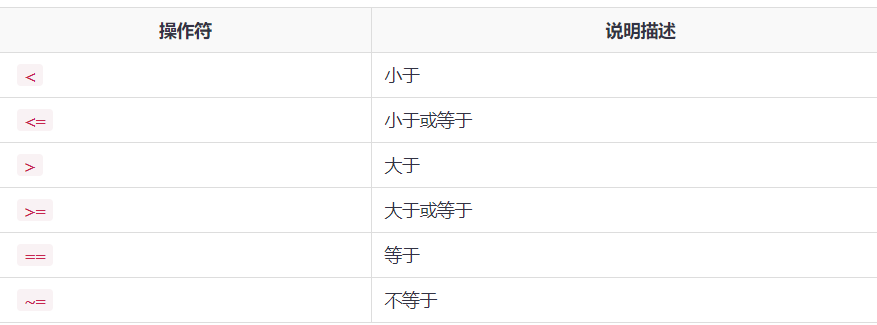
关系运算符

image-20220811234004532

逻辑运算符

& 与
**\ ** 或
~ 非

复数运算

image-20220811234632087

1
2
3
4
5
6
7
8
9
10
11
>> complex(1, 2)

ans =

   1.0000 + 2.0000i

>> 1+2i

ans =

   1.0000 + 2.0000i

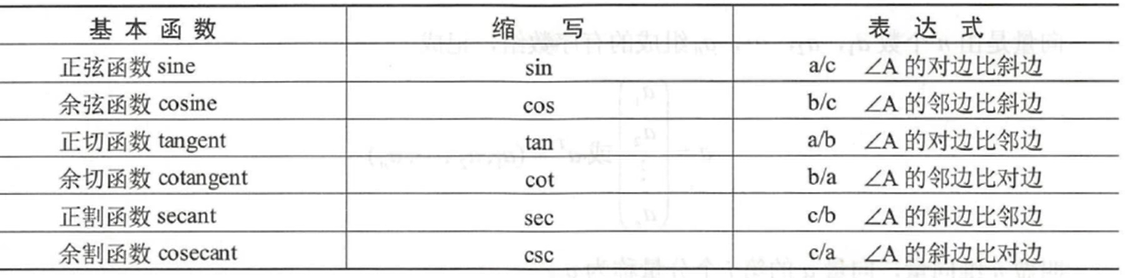
三角函数

image-20220811234829122

反三角函数asin、acos、atan

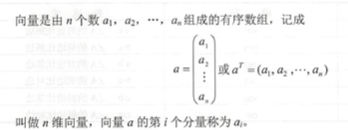
向量

image-20220811235447898

创建向量

直接创建

1
2
3
4
5
6
7
8
9
10
11
12
13
>> a = [1, 2, 3]  % 行向量

a =

     1     2     3

>> b = [1;2;3] % 列向量

b =

     1
     2
     3

冒号法(对增量要求)

x = 0:2:10

输出x = 0 2 4 6 8 10

y = 10:-3:1

输出y = 10 7 4 1

linspace（对数量要求）

x = linspace(0,10,5)

输出x = 0 2.5000 5.0000 7.5000 10.0000

x = linspace(100, 0, 5)

输出x = 100 75 50 25 0

向量元素的引用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
> x = 0: 10
x =
     0     1     2     3     4     5     6     7     8     9    10
>> x(3)  % 下标从1开始
ans =
     2
>> x(2:5)
ans =
     1     2     3     4
>> x(2:2:10)
ans =
     1     3     5     7     9
>> 2:2:10
ans =
     2     4     6     8    10
>> a = [6, 2, 11];
>> x(a)
ans =
     5     1    10
>> x([2:5 a])
ans =
     1     2     3     4     5     1    10

向量运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
>> x = 0:2:10
x =
     0     2     4     6     8    10
>> y = 0:1:5
y =
     0     1     2     3     4     5
>> x+y   % 维度一直
ans =
     0     3     6     9    12    15
>> x-y	 % 维度一直
ans =
     0     1     2     3     4     5
>> x.*y  % 维度一直
ans =
     0     2     8    18    32    50
>> x./y	 % 维度一直
ans =
   NaN     2     2     2     2     2
>> dot(x,y)	% 点积
ans =
   110
    
>> a = 1:3
a =
     1     2     3
>> b = 2:4
b =
     2     3     4
>> cross(a,b) % 叉积向量必须是三维，求出与两个向量想垂直的向量（法向量）
ans =
    -1     2    -1
>> c = [7 5 1]
c =
     7     5     1
>> dot(a, cross(b,c)) % 混合积先叉积在点积
ans =
     2

多项式

创建多项式

直接创建

1
2
3
>> 'a*x^n+b*x^(n-1)'
ans =
    'a*x^n+b*x^(n-1)'

poly2sym

1
2
3
4
5
6
7
8
9
10
>> p = [3, 4, 5, 7]
p =
     3     4     5     7
>> poly2sym(p)
ans =
3*x^3 + 4*x^2 + 5*x + 7
>> a = [2 3 4 0 0 0 1];
>> poly2sym(a)
ans =
2*x^6 + 3*x^5 + 4*x^4 + 1

根据跟来构建多项式

1
2
3
4
5
6
7
>> root = [1 -1];
>> p=poly(root)
p =
     1     0    -1
>> poly2sym(p)
ans =
x^2 - 1

多项式运算

加法和减法运算

同向量的加减法运算，维度需要一致，用0补齐

乘法运算(conv)

1
2
3
4
5
6
7
8
>> p1=[1 2];
>> p2=[3 4];
>> conv(p1, p2)
ans =
     3    10     8
>> poly2sym(conv(p1,p2))
ans =
3*x^2 + 10*x + 8

除法运算(deconv)

1
2
3
4
5
>> [k, r]=deconv(p1, p2)
k =
    0.3333
r =
         0    0.6667

求导（polyder）

1
2
3
4
5
6
7
>> p = [2 3 8 -5 6];
>> poly2sym(p)
ans =
2*x^4 + 3*x^3 + 8*x^2 - 5*x + 6
>> q=polyder(p)
q =
     8     9    16    -5

多项式求解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
>> p = [2 3 1];
>> poly2sym(p)
ans =
2*x^2 + 3*x + 1
>> roots(p)
ans =
   -1.0000
   -0.5000
%-------------------------------
>> syms x	% 声明变量
>> f = x^2+x-1==0	% 输入方程
f = 
x^2 + x - 1 == 0
>> solve(f)
ans =
- 5^(1/2)/2 - 1/2
  5^(1/2)/2 - 1/2
>> vpa(ans)	% 转化成小数
ans =
-1.6180339887498948482045868343656
0.61803398874989484820458683436564
>> double(ans)	% 精度
ans =
   -1.6180
    0.6180

单元型变量

单元型变量是以单元为元素的数组，每个元素称为单元，每个单元可以包含其他类型的数组，如实数矩阵、字符串、复数向量。单元型变量通常由“”创建，其数据通过数组下标来引用。（可包括不同的数据类型）

创建、引用及赋值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
>> a = 2;
>> b = [1, 2, 3];
>> c = 'abc';
>> d = 3+2i;
>> e = {a, b, c, d}
e =
  1×4 cell 数组
    {[2]}    {[1 2 3]}    {'abc'}    {[3.0000 + 2.0000i]}
>> e{1}	% 引用
ans =
     2
%-----------------------------
>> e=cell(1, 3)	% 生成空cell
e =
  1×3 cell 数组
    {0×0 double}    {0×0 double}    {0×0 double}
>> e{1,1}=[1,2;3,4]
e =
  1×3 cell 数组
    {2×2 double}    {0×0 double}    {0×0 double}
>> e{1,2}='cfg'
e =
  1×3 cell 数组
    {2×2 double}    {'cfg'}    {0×0 double}
>> e{1,3}=2
e =
  1×3 cell 数组
    {2×2 double}    {'cfg'}    {[2]}

相关函数

image-20220812101238471

1
2
3
4
5
6
7
8
9
10
11
12
>> s = '123'
s =
    '123'
>> str2num(s)
ans =
   123
>> class(s)
ans =
    'char'
>> class(str2num(s))
ans =
    'double'

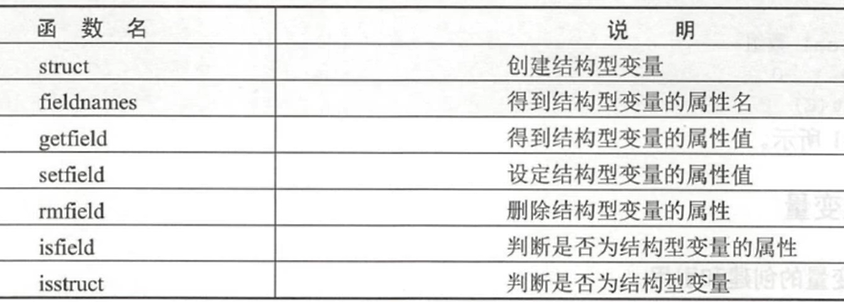
结构性变量

结构型变量是根据属性名(field)组织起来的不同数据类型的集合。结构的任何一个属性可以包含不同的数据类型，如字符串、矩阵等。结

构型变量用函数 struct来创建。

image-20220812102005272

创建、引用及赋值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
>> m=struct('color',{'red','blue'},'number',{1,2},'str','a')
m = 
  包含以下字段的 1×2 struct 数组:
    color
    number
    str
>> m(1)
ans = 
  包含以下字段的 struct:
     color: 'red'
    number: 1
       str: 'a'
>> m(1,2)
ans = 
  包含以下字段的 struct:
     color: 'blue'
    number: 2
       str: 'a'
>> m(1).color
ans =
    'red'
>> m.color
ans =
    'red'
ans =
    'blue'

相关函数

image-20220812102434344

矩阵

image-20220812102635984

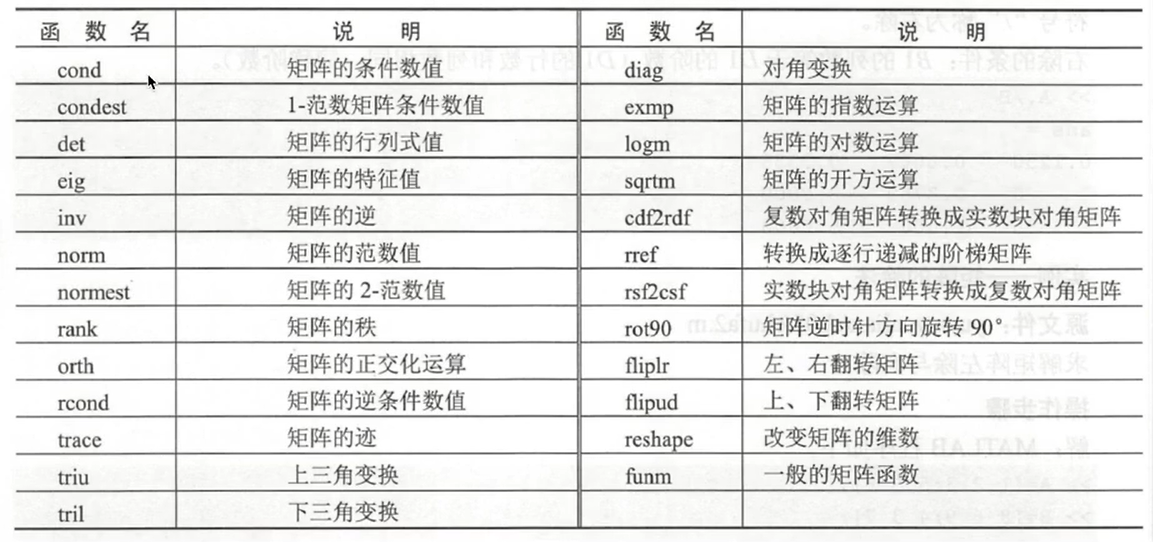
矩阵创建

矩阵创建是注意：

  • 输入矩阵时要以“[]”为其标识符号，矩阵的所有元素必须都在括号内。
  • 矩阵同行元素之间由空格（个数不限）或逗号分隔，行与行之间用分号或回车键分隔。矩阵大小不需要预先定义。
  • 矩阵元素可以是运算表达式。
  • 若“[]”中无元素，表示空矩阵。
  • 如果不想显示中间结果，可以用“;”结束。

直接创建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
>> a = [1, 2; 3, 4]
a =
     1     2
     3     4
%--------------------------
>> load test.txt	% 通过txt文件导入
>> test	% 变量以文件名为名
test =
     1     2     3
     4     5     6
     7     8     9
>> class(test)
ans =
    'double'
>> test(1,:)	# 提取第一行
ans =
     1     2     3
>> test(:,1)	# 提取第一列
ans =
     1
     4
     7

函数创建

image-20220812104035587

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
>> eye(3)
ans =
     1     0     0
     0     1     0
     0     0     1
>> eye(3,4)
ans =
     1     0     0     0
     0     1     0     0
     0     0     1     0
>> ones(3)
ans =
     1     1     1
     1     1     1
     1     1     1
>> ones(3,1)
ans =
     1
     1
     1
>> zeros(3)
ans =
     0     0     0
     0     0     0
     0     0     0
>> zeros(3,1)
ans =
     0
     0
     0
>> rand(3)
ans =
    0.8147    0.9134    0.2785
    0.9058    0.6324    0.5469
    0.1270    0.0975    0.9575
>> rand(2,3)
ans =
    0.9649    0.9706    0.4854
    0.1576    0.9572    0.8003
>> n = [1,2,3]
n =
     1     2     3
>> diag(n)
ans =
     1     0     0
     0     2     0
     0     0     3
>> hilb(3)
ans =
    1.0000    0.5000    0.3333
    0.5000    0.3333    0.2500
    0.3333    0.2500    0.2000
>> magic(3)	%魔方矩阵每行每列及对角线之和相等
ans =
     8     1     6
     3     5     7
     4     9     2

矩阵引用及修改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
>> test
test =
     1     2     3
     4     5     6
     7     8     9
>> e=[6;4;7];
>> f=[1, 3, 3, 4];
>> a=[test, e; f]
a =
     1     2     3     6
     4     5     6     4
     7     8     9     7
     1     3     3     4
%--------------------------------
>> a(3,2)	% 第3行第2列
ans =
     8
>> a(3,[2, 1, 3])	% 第3行第2/1/3列
ans =
     8     7     9
>> a(2,:)	% 第二行所以元素
ans =
     4     5     6     4
>> a(:,3)	% 第3列所有元素
ans =
     3
     6
     9
     3
>> a(2,:)=[]	% 删除第2行
a =
     1     2     3     6
     7     8     9     7
     1     3     3     4
>> a(1,:)=[]	% 删除第1行
a =
     7     8     9     7
     1     3     3     4
>> a=[[1 2 3 6];a]	% 添加元素
a =
     1     2     3     6
     7     8     9     7
     1     3     3     4
>> a(:,1)=[]	% 删除第1列
a =
     2     3     6
     8     9     7
     3     3     4

矩阵运算

变维(reshape)

1
2
3
4
5
6
7
8
>> a = 1:12
a =
     1     2     3     4     5     6     7     8     9    10    11    12
>> reshape(a,3,4)
ans =
     1     4     7    10
     2     5     8    11
     3     6     9    12

加减运算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
>> a = [1:3;6:8;4:6]
a =
     1     2     3
     6     7     8
     4     5     6
>> b=[1, 3, 4];
>> a+b
ans =
     2     5     7
     7    10    12
     5     8    10
>> a-b
ans =
     0    -1    -1
     5     4     4
     3     2     2

乘法运算

image-20220812114841186

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
a =
     1     2     3
     4     5     6
     7     8     9
>> b=a;
>> a.*b
ans =
     1     4     9
    16    25    36
    49    64    81
>> a*b
ans =
    30    36    42
    66    81    96
   102   126   150

image-20220812115308681

image-20220812120036281

image-20220812120540240

1
2
3
4
5
6
7
8
9
>> p=3.4
p =
    3.4000
>> sym(p)
ans =
17/5
>> eval(ans)
ans =
    3.4000

转置（’或traspose）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>> a
a =
     1     2     3
     4     5     6
     7     8     9
>> a'
ans =
     1     4     7
     2     5     8
     3     6     9
>> transpose(a)
ans =
     1     4     7
     2     5     8
     3     6     9

行列式求值(det)

1
2
3
4
5
6
7
8
>> syms x y z	% 声明变量
>> a = [x, y; z, x]
a =
[x, y]
[z, x]
>> det(a)
ans =
x^2 - y*z

特征值、特征向量(eig)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
a =
     2     5     7
     7    10    12
     5     8    10
>> [c, d] = eig(a) %  c的每一列值表示矩阵a的一个特征向量，这里有3个特征向量，d的对角元素值代表a矩阵的特征值
c =
    0.3649    0.8407    0.3244
    0.7267   -0.5414   -0.8111
    0.5820    0.0115    0.4867
d =
   23.1244         0         0
         0   -1.1244         0
         0         0    0.0000
>> diag(d)	% 取出d的对角线元素值，也就是a矩阵的特征值
ans =
   23.1244
   -1.1244
    0.0000

矩阵的秩(rank)

1
2
3
4
5
6
7
8
9
10
11
12
>> help rank
 rank - 矩阵的秩
    此 MATLAB 函数 返回矩阵 A 的秩。
    k = rank(A)
    k = rank(A,tol)
    See also sprank, svd, orth, null
    rank 的文档
    名为 rank 的其他函数
    
>> rank(a)
ans =
     2

符号与数值

符号声明（syms）

syms x y z

image-20220812121934583

符号展开(expand)

1
2
3
4
5
6
7
>>`syms x
>> a = (x+3)^4
a =
(x + 3)^4
>> expand(a)
ans =
x^4 + 12*x^3 + 54*x^2 + 108*x + 81

符号简化(simplify)

1
2
3
4
5
6
>> b = sin(x)^2 + cos(x)^2
b =
cos(x)^2 + sin(x)^2
>> simplify(b)
ans =
1

分式通分(numden)

1
2
3
4
5
6
7
8
9
>> syms x y
>> a = x/y - y/x
a =
x/y - y/x
>> [n, d]= numden(a)
n =
x^2 - y^2
d =
x*y

代入数值(subs)

1
2
3
4
5
6
7
8
9
10
11
12
>> z = [x+y, x;y x-y]
z =
[x + y,     x]
[    y, x - y]
>> subs(z, x, 1)	% 部分代入
ans =
[y + 1,     1]
[    y, 1 - y]
>> subs(z, [x, y], [1, 2])	% 全部代入
ans =
[3,  1]
[2, -1]
Matlab
上一篇:
C++项目通讯管理系统
下一篇:
神经网络-搭建小实战
本文目录
本文目录
    •

    Copyright © 2019 - 2020 yuang01 | Powered by Hexo | Theme Bamboo

    本站总访问量： 次 |