有限元分析学习二

第一、二、三强度理论

第一强度理论:最大拉应力准则

基本观点:材料中的最大拉应力到达材料的正断拉力时，即产生脆性断裂。适用范围:铸铁，工具钢，工业陶瓷等多数脆性材。

第三强度理论:最大剪应力准则

基本观点:材料中的最大剪应力到达该材料的剪切抗力时，即产生塑性屈服。适用范围:低碳钢、铜、软铝等塑性较好材料。

第四强度理论:形状改变比能准则

基本观点:材料中形状改变比能到达该材料的临界值时，即产生塑性屈服。

适用范围:它既突出了最大主应力对塑性屈服的作用，又适当考虑了其它两个主应力的影响，它与塑性较好材料的试验结果比第三强度理

论符合得更好。

安全系数图解

结果->安全系数

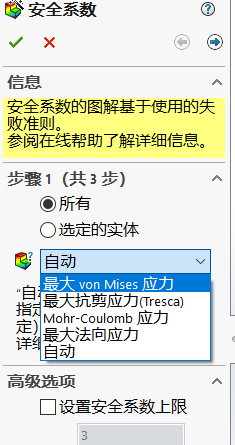
除了Mohr-Coulomb应力，其他分别对应第一二三强度

以最大von Mises应力为例：

安全系数图解反过来看，看最小值，最小是最危险的地方

四大强度理论公式

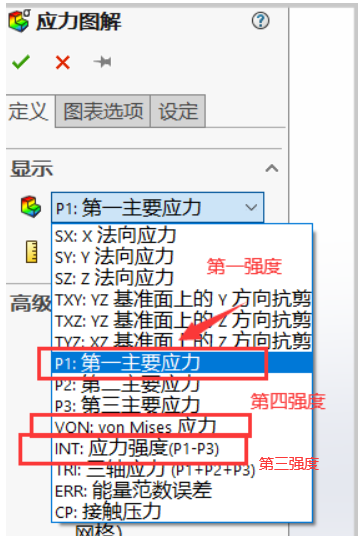
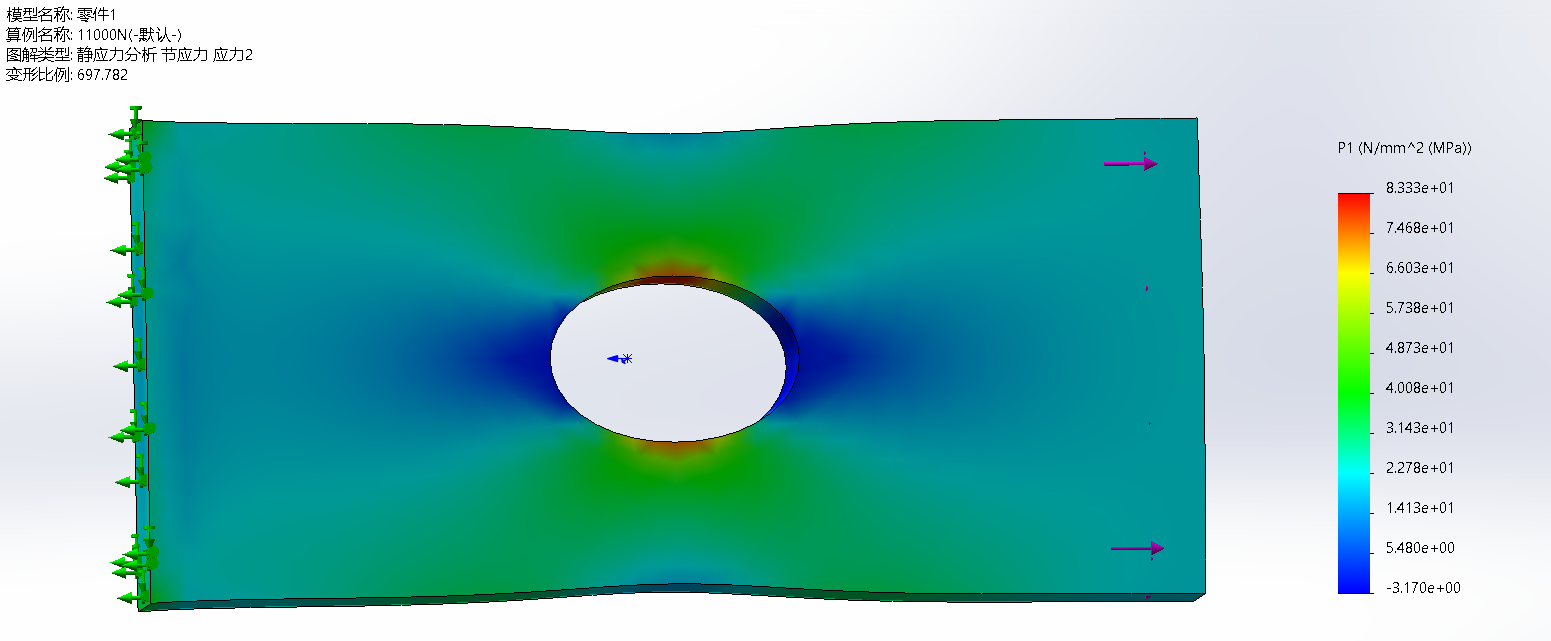
第一强度理论分析（P1）

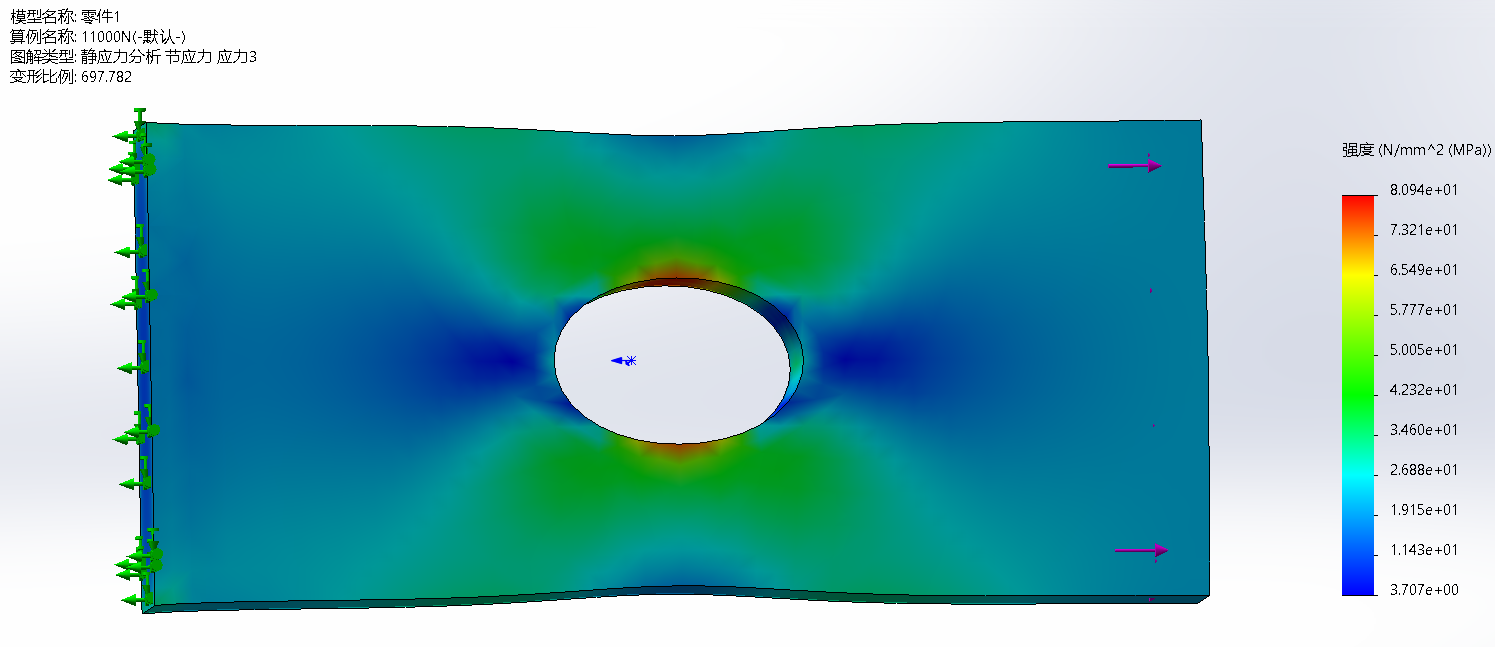
第三强度理论分析（P1-P3）

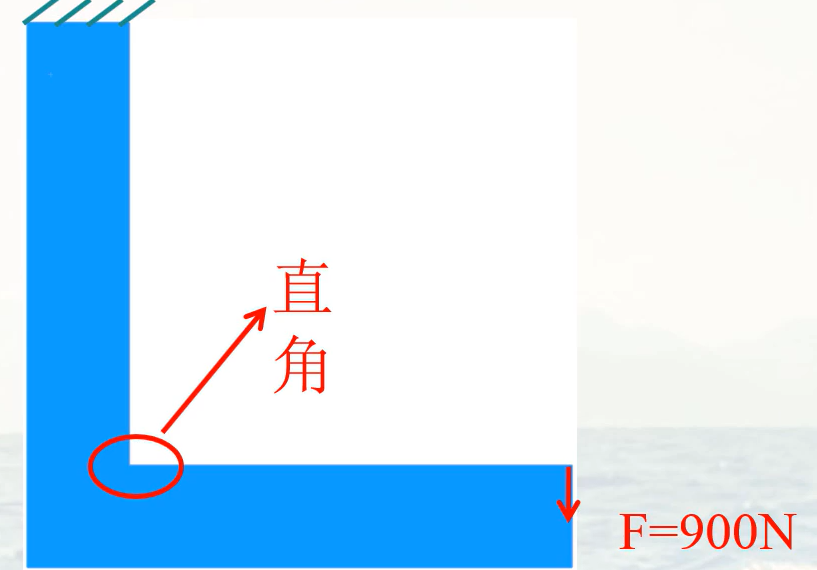
直角L型支架的应力分析

题目

问题描述：L型支架上端面固定，同时在下端面施加900N弯曲载荷，分别使用10mm、3mm和1mm网格求解模型，对比应力结果

材料: AISI 304

创建新算例

选择材料AISI 304

夹具固定约束端

添加外部载荷力的大小和方向

生成网格

设置网格参数分别为10mm,3mm,1mm

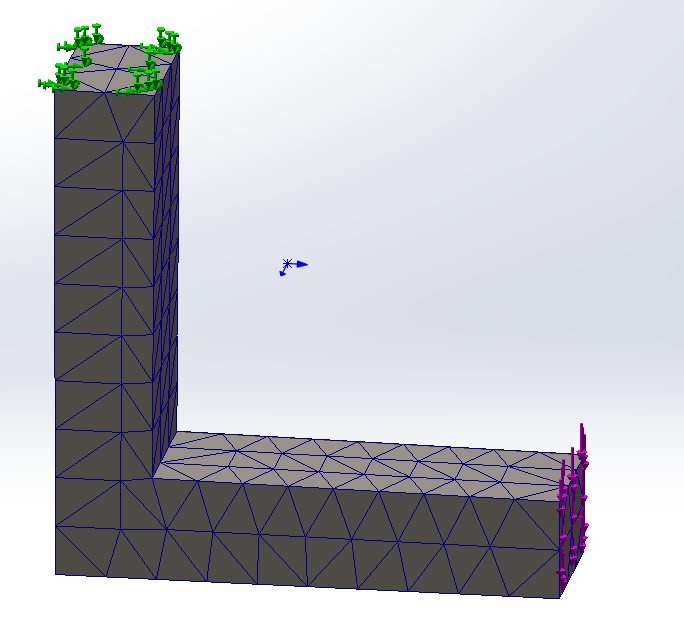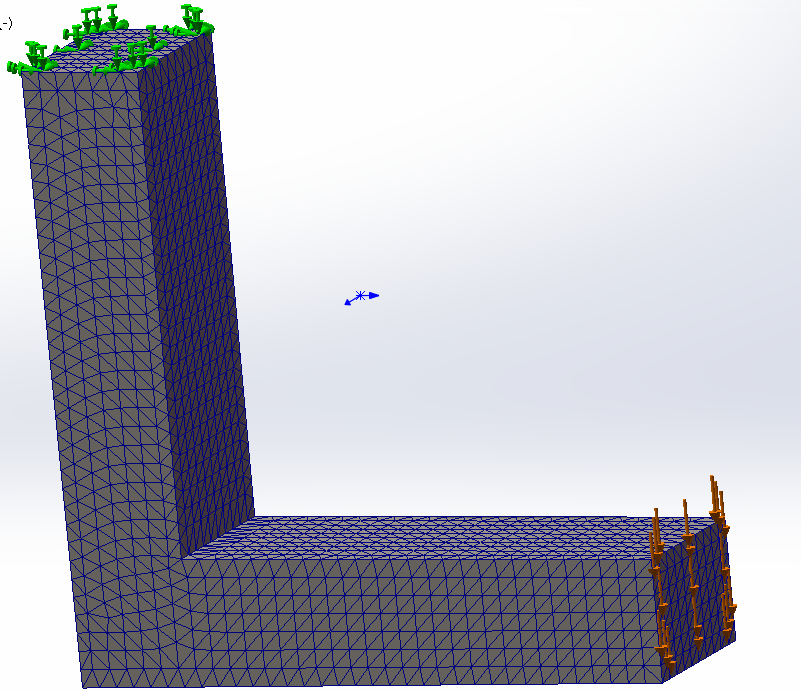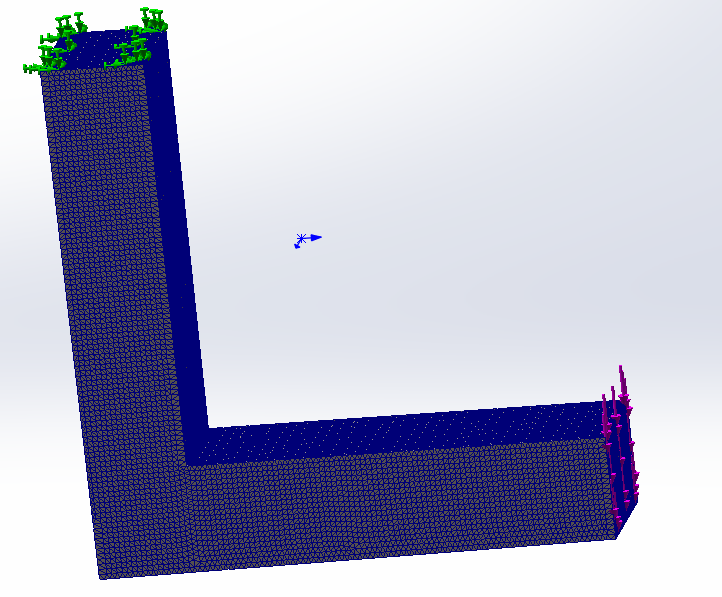10mm	3mm	1mm

运行计算

复制算例，分别更改网格大小10mm,3mm,1mm，进行对比分析

10mm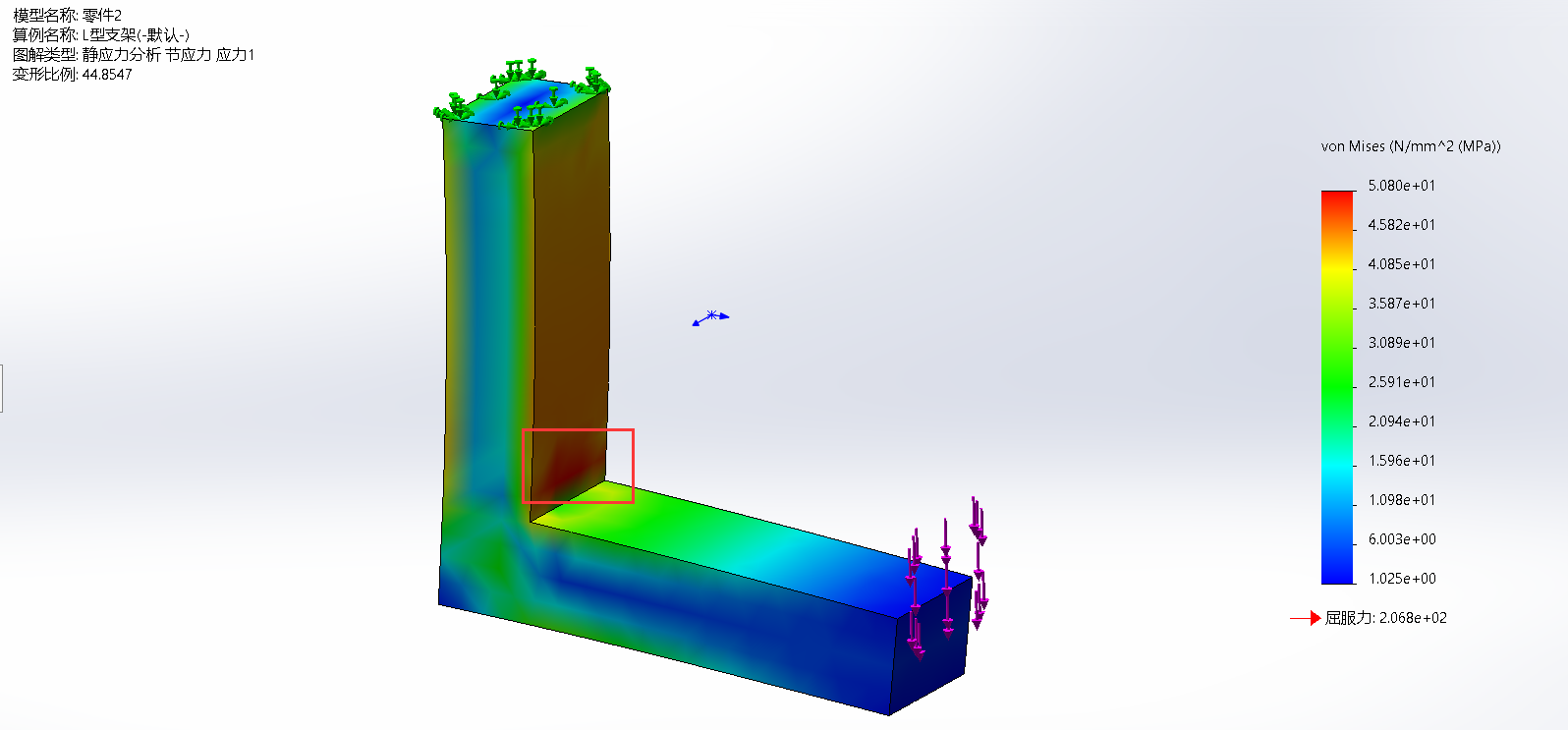

3mm

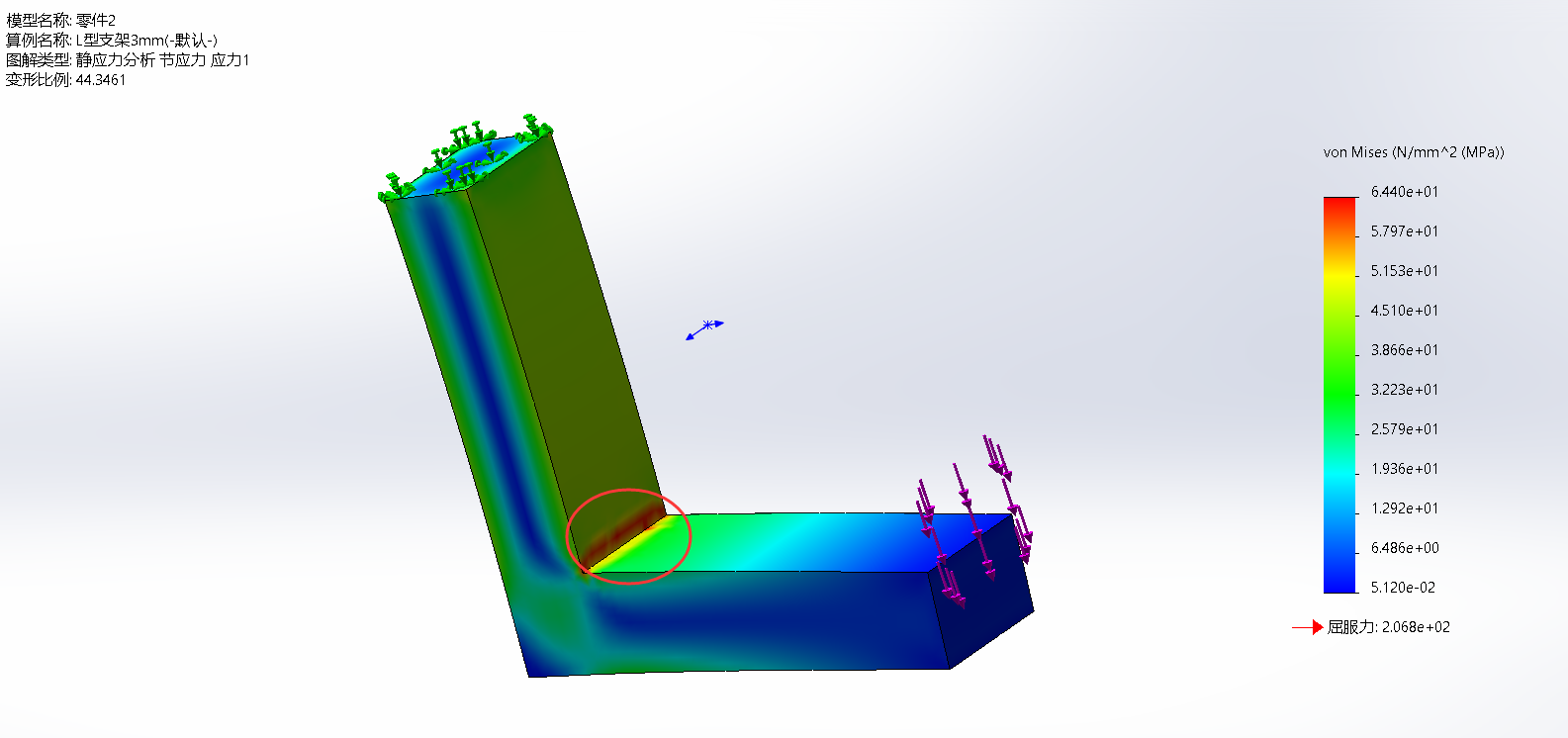
1mm

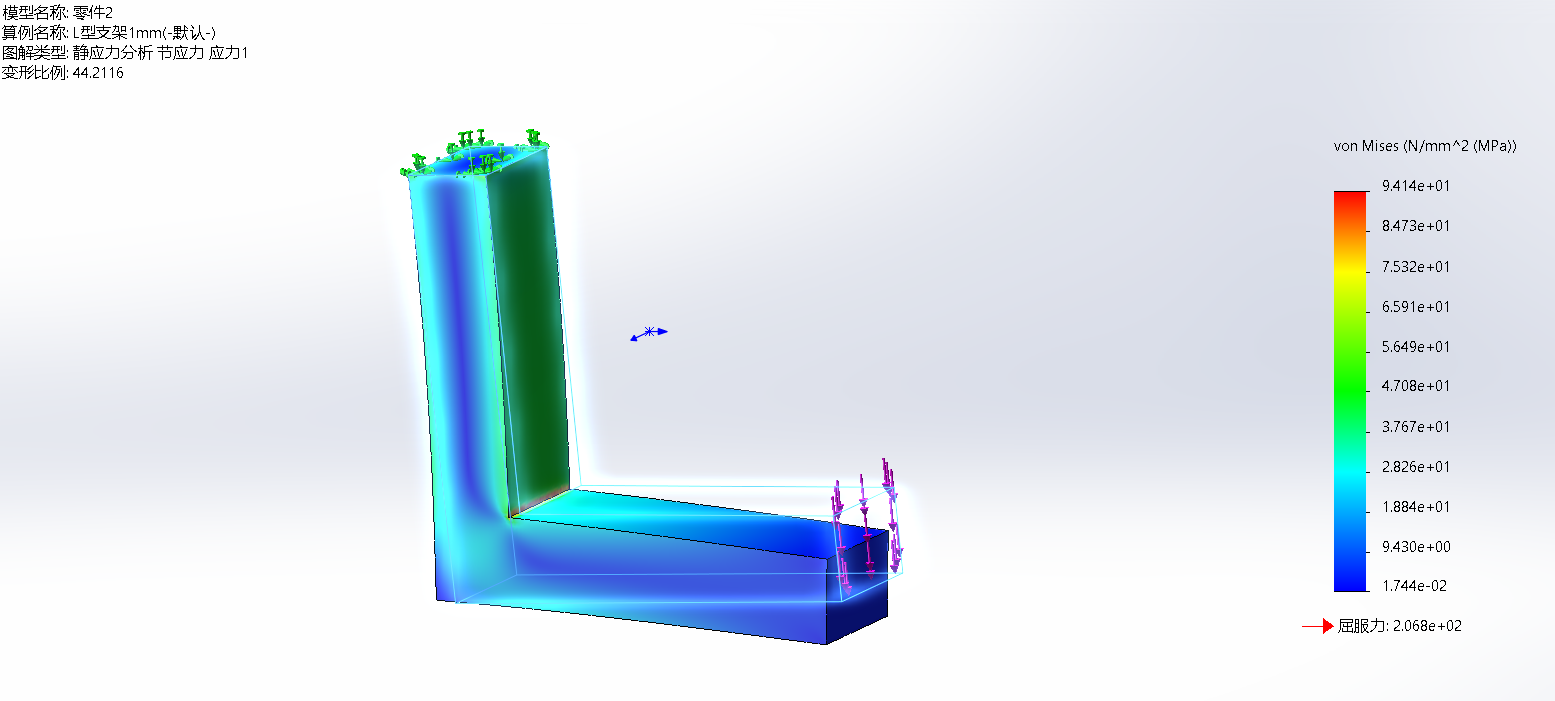
L型支架加上圆角

问题描述:L形支架上端面固定，同时在下端面施加900N弯曲载荷，分别使用10mm、2mm和0.5mm网格求解模型，对比应力分布和位移分布情况。

材料: AISI304

应力结果

10mm

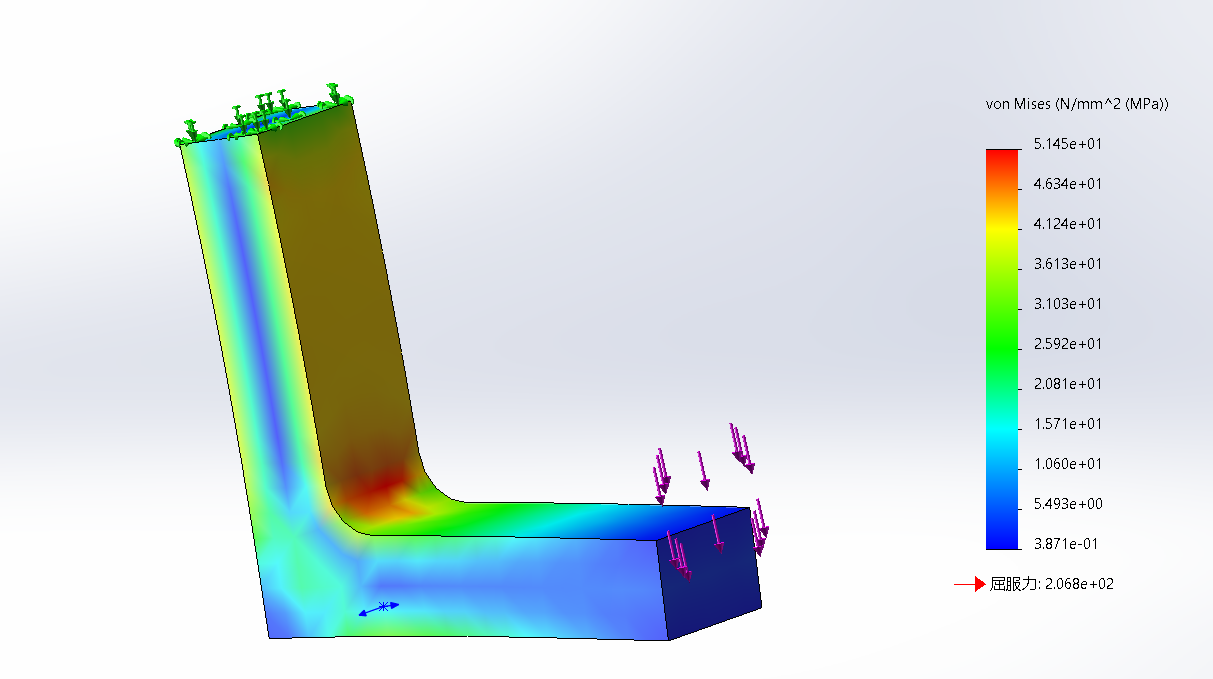
局部网格

网格->应用网格控制

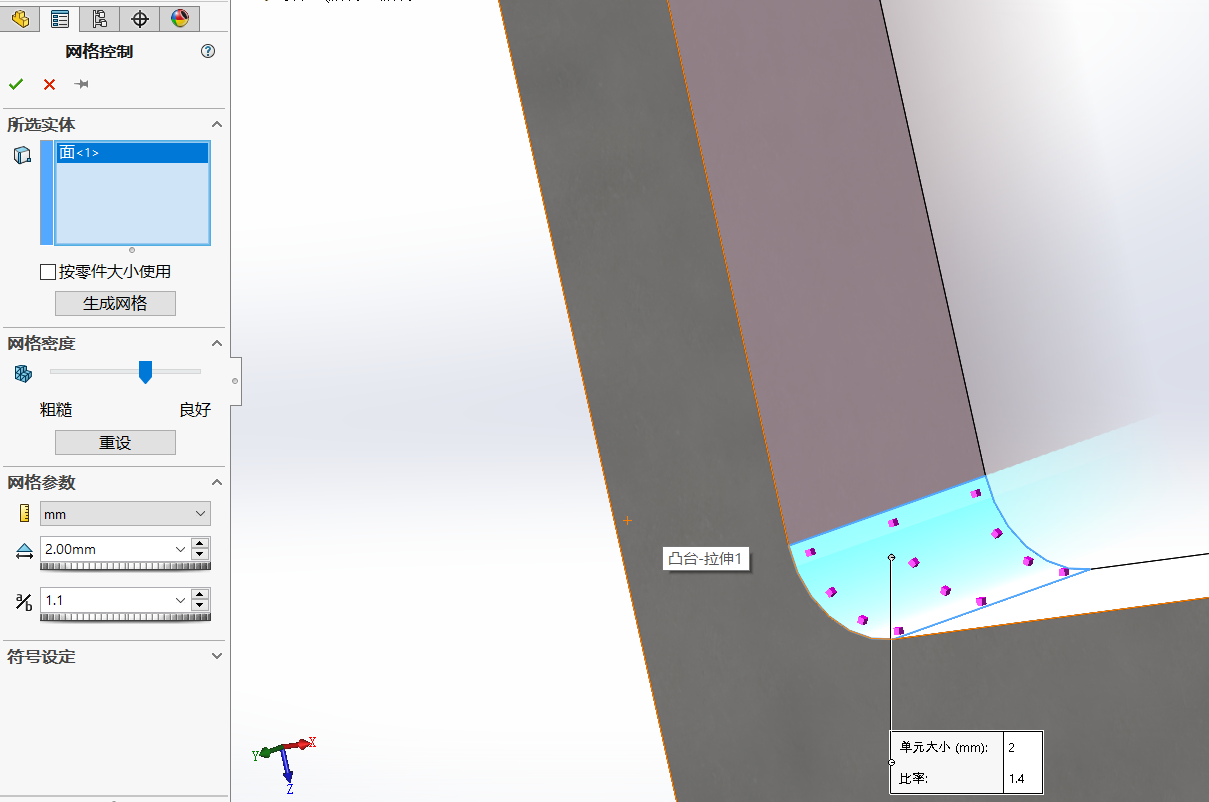
选择想要加网格面，设置网格大小，a/b的意思为网格变化的渐进过程大小

很明显可以看到网格逐步由小变大

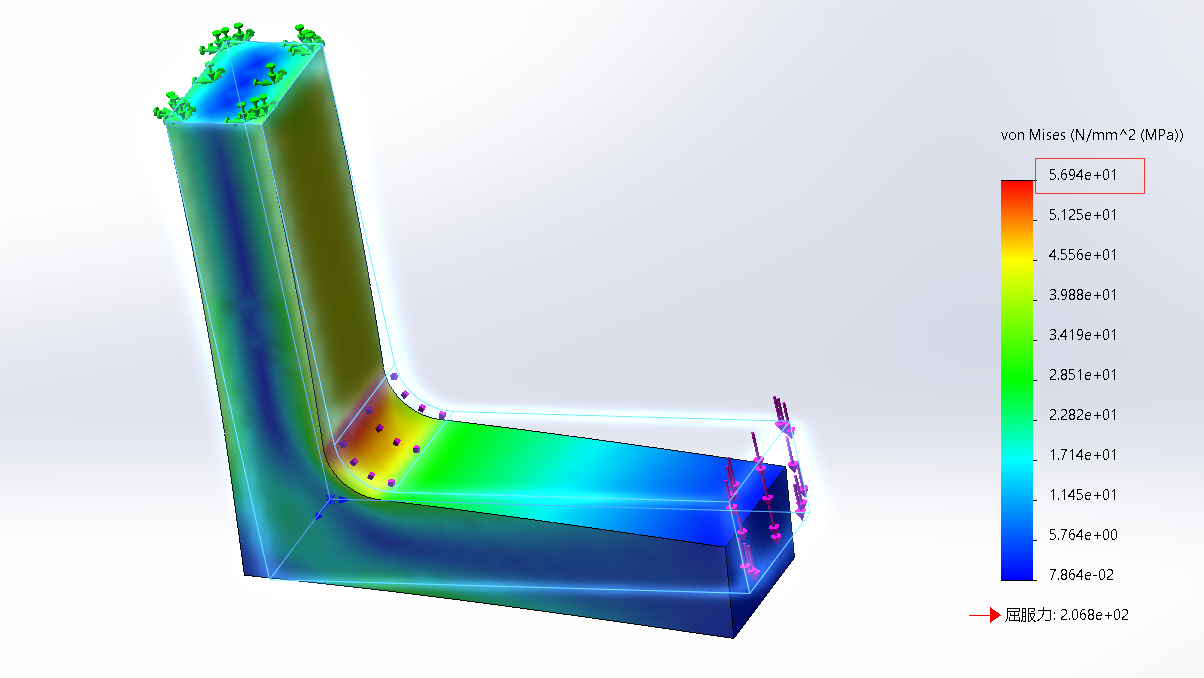
2mm

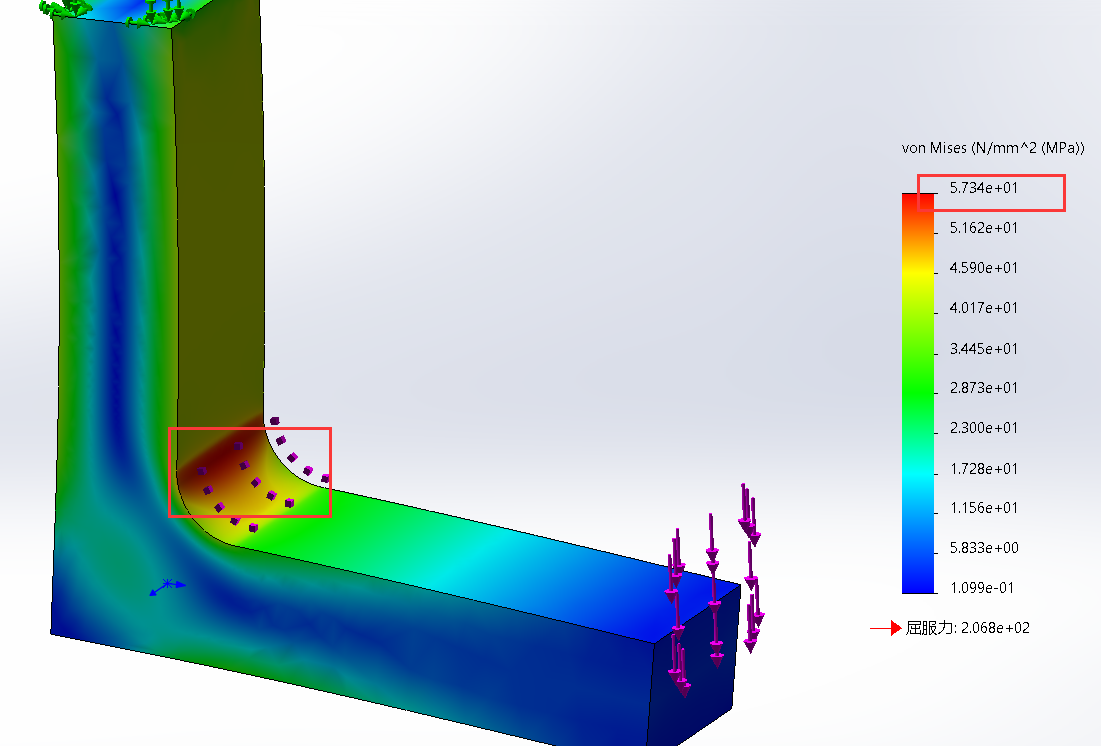
0.5mm

网格的密度影响

应力结果的网格无关性检查

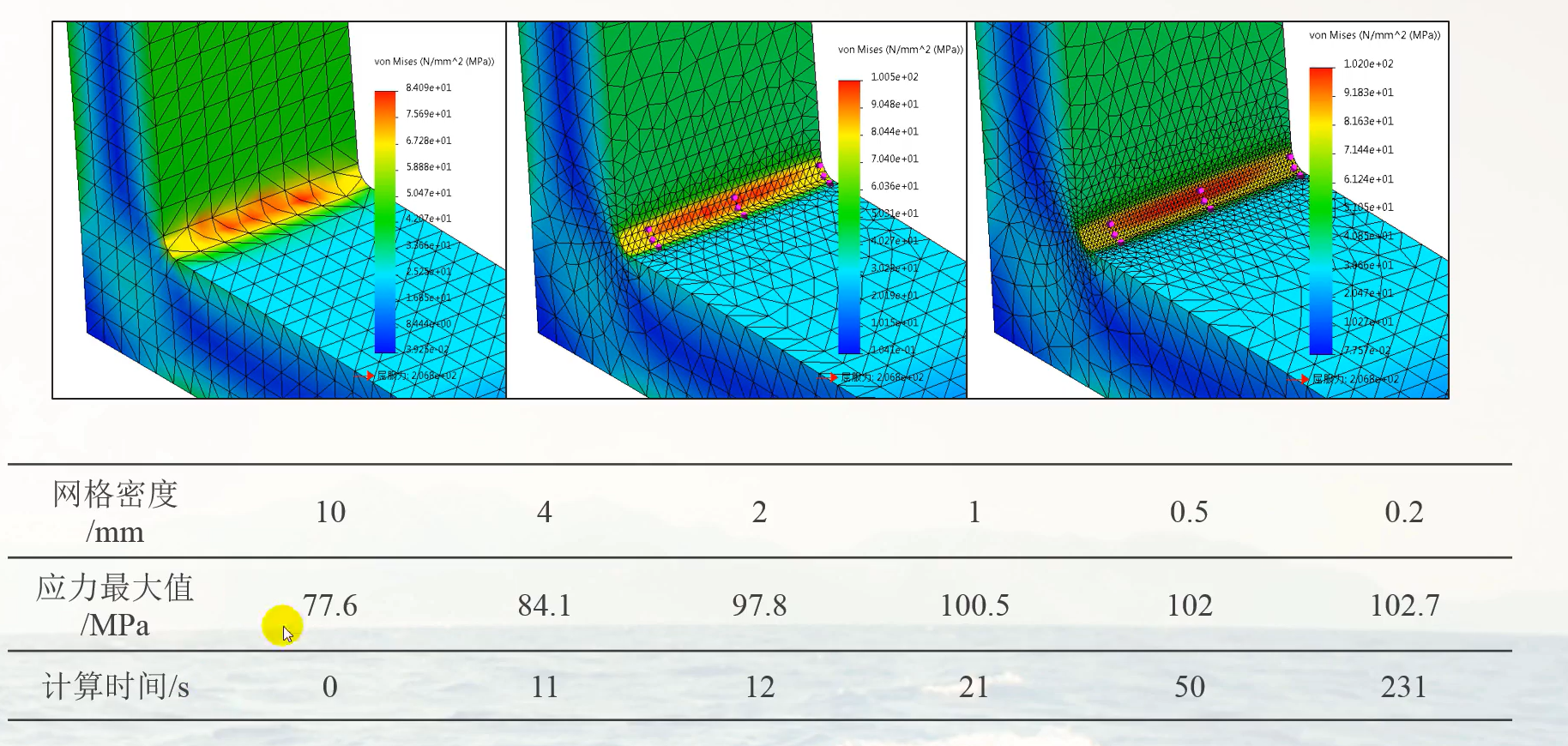
由以上分析可得，网格密度越小，其计算算例的时间就越长，才用局部网格可以缩短时间；而应力的结果受网格的精度影响很大。

位移影响与网格密度

位移影响与网格密度不大。